I’ve been thinking a lot about maths recently. We were sat in the lounge as a family this week and it was nearly time for bed when we realised that my seven year old can read an analogue clock. This sort of popped up, we knew she sort of got it, but suddenly (or at least to us from our perspective) she just announced through competency that she can tell the time. It again confirmed that, like percentages and fractions and place value, her knowledge of mathematics often exceeds what I feel I have may have “taught her” and that she really is just learning like the Rotuman of the South Pacific believe children do, by sniffing around like dogs what is useful in the culture and then devouring it.
I’m a maths specialist by training and it is a part of self-directed education that I think about a lot. I’ve already written about how children who are self-directed learn to read, but how do you learn maths as a self-directed young person, and more to the point how can adults around you best support you, and then to follow that out more broadly how would maths be approached in a culture where self-direction was the norm rather than the exception?
This reflection could be seen as a place holder for a more detailed analysis of the above questions, but this week at work there was an hour of maths activities that looked an awful lot like play and, akin to a literacy community of practice, offered a glimpse of what a mathematical community of practice looks like.
Myself and another mentor found an old primary school mathematics resource pack from the early 2000’s which interested us mostly because of the VHS1 that it came with. We sat around in the lounge - our open sided yurt - discussing our memories of VHS tapes in secondary schools from around the same time. No children were present here as they were all inside the actual yurt sensibly keeping warm, whilst we ate our lunch in the cold.
We were flicking through the teacher resource pack when we came across this question:
A shepherd has three pens of different sizes, small, medium and large and 24 sheep. The sheepdog has to herd them into the pens but no one pen can have the same amount of sheep.
How many possible combinations are there if each pen can only have even amounts of sheep in it?
I invite you to pause here, grab a pen and paper if needed and have a go yourself. It should take no more than five minutes.
For context this was a question for eight to nine year olds. In the setting of a classroom I don’t think this question is too bad, but it is obviously a contrived and decontextualised question, but context is everything and in the hands of two maths teachers at a self-directed learning community it is a different beast. Suddenly it becomes a puzzle for playing with. We riffed on the question.
I wonder why it is only even numbers?
I wonder if there are vastly more solutions if you include odd numbers?
Maybe we are only looking for even solutions because there is a more manageable amount of solutions.
Maybe the odd solutions is an extension question for children who get the answer and need stretching.
Maybe, or maybe a systematic approach to solutions is clearer when you only look for even numbers? And therefore patterns are easier to see and then generalise.
Yeah, ok, I wonder how many solutions there are then?
So I proposed a method. I reasoned that most of the solutions would centre around eight so I started with the non-solution of putting eight sheep in each pen and then moving them around from there.
Did you get the same amount of solutions?
There are 7 solutions using only even numbers.
Then we moved on to wondering what the number of solutions would be if there were odd numbers included. At first we wondered if you would just double the amount of solutions. But then realised that there was only really one way to find out, by again writing them down and checking them. So we did. Here we divulged. They used the method that we had previously used for only even numbers, working outwards from eight as the middle number whilst I briefly started with that but then decided to use a different method.
Intuitively I had reasoned that starting with a non-solution of three eights was reasonable for even numbers as eight would be the middle pen number with the greatest amount of solutions, but for some reason I changed my method and instead of starting from reasoning which middle pen would have the maximum amount of solutions I looked for the maximum solution for the largest pen and worked systematically from there downwards. And in doing so noticed an interesting pattern.
The number of solutions progresses in steps. The two largest pens have one solution each, the next two largest pens have two solutions each, the next two three solutions and so on. I noticed that each time there was an even number in the largest pen there was a solution that wasn’t valid where the small and medium pen held the same amount - these are circled below.
This pattern continued until we got to twelve as the largest pen number, and then from eleven onwards the pattern no longer held. Here we started to get solutions that were actually repeats of previous solutions and also not valid because obviously twelve can’t be in the medium pen and eleven in the largest pen.
This gives us a total of 37 solutions for pens that can include odd numbers.
Mathematics as Community of Practice
So how do young people learn maths when self-directing themselves? All this maths took us around twenty minutes. But no one was there to witness it. But I think that that is key to how young people learn maths as situated learners in a community of practice. When talking about work and education before I said that we needed to find ways in which we can have an open book approach to our culture and connect young people with competent adults.
This is the open book approach to mathematics culture as opposed to the black box that schools offer. Ironically using a question taken from a school curriculum.
The reason it is key that no one was there to witness it is because none of this is performative or contrived. This is maths being explored for fun by people competent at maths in a setting where any young person could have come along at any time and sniffed around what was going on and devoured it. Would we have changed what we were doing if someone had joined us? Somewhat, yes, obviously. But the bones of it would have been the same. Would we have found ways to modify parts and interject with appropriate questions to fit the zones of proximal development of the young people that showed an interest, yes. But would we both have wanted to get the answer to how many sheep in each pen when an odd number of sheep were allowed in each pen, yes. Would we have wanted to get there with an elegant solution, therefore modeling ways in which patterns can jump out of questions if you think about how to approach them systematically. Yes!
This twenty minutes contained a lot of maths but more importantly so much potential for maths talk. So many rich possible questions that could have popped out of this puzzle if a young person had come along and shown an interest ranging from the simple difference between even and odd numbers for someone five or six to something much more complex for a teenager.
But what might that look like? How can a question for eight year olds be mathematically rich for teenagers? In maths pedagogy this is called low floor high ceiling.
I thought about what the most complex maths that could be pulled out of this question could be whilst writing this. One of the things that I enjoy doing with maths is finding different ways of representing the same thing mathematically. Often that is thinking about how can we show graphically what is going on with algebra and numbers? GeoGebra is a great piece of software for this and maybe we could use it to model this question on computer graphing software and discuss more deeply what is going on.
I was thinking about the instance where the answers were progressing down in sets of two: two largest pens had one solution each, next two largest had two solutions each, and so on. And thinking about the instances where the small and medium pen held the same number that I had circled above. Could we see those instances graphically? I played around and in ten minutes had built something out.
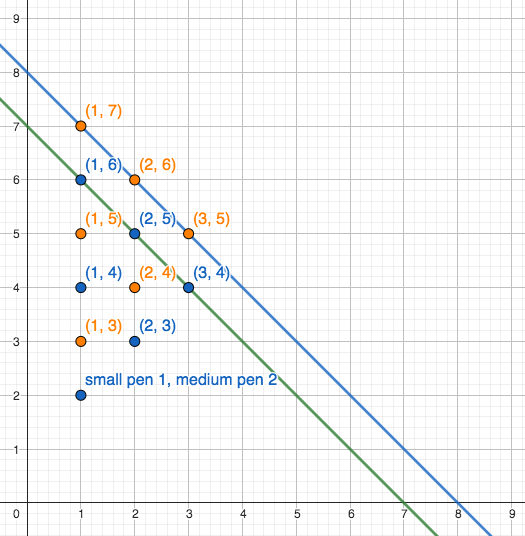
We could start off by plotting the solutions on a graph - the x-axis representing the smallest pen and the y-axis representing the middle pen. The solution for when the largest pen has a maximum solution is labelled small pen 1, medium pen 2. Here we have the first nine solutions from the first five numbers we chose to be the largest pen: 21, 20, 19, 18, and 17.
We might then notice, due to using different colours that they are all on the diagonal. When the largest pen is 17, the other two pens obviously have to add up to seven: (1,6); (2,5); (3,4). Both these pieces of information can lead us to the straight line x+y=7. And then the line x+y=8 which all the next solutions lie upon.
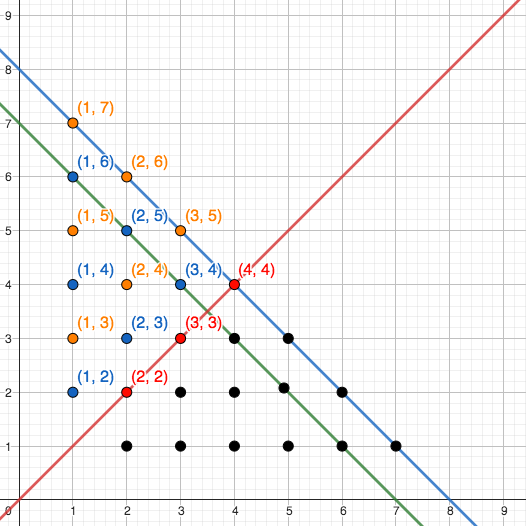
At this point maybe we put in some of the non-solutions that we found earlier that we found interesting, when both the smaller pen and the middle pen were the same. And then we might reason they lie on a line also.
Here we are getting towards discussions on the mathematical concept of areas bounded by a line. So far every solution lies between the red line y=x and the y-axis. We could also see that the line y=x is a line of symmetry for the same amount of solutions lying between it and the x-axis as represented by the black dots.
Now we can follow the pattern we had earlier and build it out. Remembering that at some point the pattern stopped (at two sets of 5 solutions) and then we had a gradual reduction until for 9 as the largest pen there was only one solution: 7, 8, 9. We could use more lines to build the pattern up or just input the solutions without; I will do without.
Similar to when the smaller pen and the middle pen were equal and therefore non-solutions we also have non-solutions where the larger and middle pen were the same. These non-solutions are represented by the black dots and they also fall on a line: y=-0.5x+12. This line seems to be the boundary for all possible solutions.
And here the maths can really begin as we have the opportunity to move from abstraction to generalisation.
If we change the number of sheep how can we predict the number of solutions?
Is the red line y=x always going to be a boundary?
The black line has 0.5 and 12 in and together they relate to the total number of sheep, 24, why might that be?
Would there always be a black boundary line and what might always be similar about it and what might be different?
We looked at diagonal lines through the solutions, what about vertical or horizontal lines?
Could you make predictions about when there were 12 sheep instead of 24 and test them with GeoGebra?
If you know how to use GeoGebra this would take less than ten minutes to plot out whilst slowly walking through the reasoning for each step. Obviously if you need to go slower you can. This is rich and deep maths. Taking a simple problem and stretching it to demonstrate both the powerful maths you can find within it and the powerful mathematical tools that computers now allow us to use to play around with mathematical ideas.
Mathematical thinking and mathematics culture
There was also so much possibility for mathematical thinking in this which is not about the “maths” itself; more than just massaging the numbers but the hows and whys. We were modelling the importance of asking lots of questions first before seeking answers, demonstrating that maths is done collaboratively, maths is inherently creative, there are multiple different solutions to get the “solution”, maths is beautiful (patterns are inherently beautiful), finding answers always leave you with more questions and more maths to uncover, and the importance of thinking about deriving solutions in a systematic way.
And finally, that maths, actually, believe it or not children, is enjoyable.
Mathematicians aren’t robots, crunching numbers, they are artists and that is the most important thing to learn about mathematics.
Twenty minutes was enough. We moved into the yurt and we found people playing with some other maths resources that had been taken out at the same time as the VHS pack, some Dienes blocks. These are concrete resources for thinking about addition, subtraction, multiplication and division and most usefully manipulating place value. But some of our youngest young people had used them to build robot faces. So we went along with it. They build different faces and we asked them what number each face that they had built represented. Here we have Robot-112.2
We played around with making different robots and different faces asking questions about place value hidden in questions about robot eyebrows and smiles and after fifteen minutes we were done. Often that is all that is needed. Children’s brains are wired for play, wired for learning through play, and research shows that learning happens faster when engaged in play. The brain is literally more alive and more receptive. But with play you don’t know what learning is going on, because to most people “learning” is almost the antithesis of play. Learning is when something is going on that is easily measurable and quantifiable, something that you can see taking place. But real learning is happening all the time. And at our learning community it happens through play, and so the best way that adults can relate to children is by playing. And by playing with maths we are teaching young people that maths is for playing with and therefore maths is worth learning. And that fundamentally is how self-directed young people learn maths.
This is what people used to watch stuff on before we had netflix. You had to rewind it when you had finished using it otherwise the next poor sucker to get it would have to wait for five minutes before they could watch it. And now we can’t bear five seconds of buffering.
Red blocks are worth hundred, yellow are worth ten, and green are ones. Dienes blocks work really well by allowing you to envisage the “carrying” of tens that one does with multiplication and subtraction that ties into what it means for a number to be made up of composite parts of different place values. Subtract 3 from Robot-112 and whilst the first two are easy to take away you suddenly need to break the yellow ten up into ten green unit blocks to be able to take away the final one. If you were to subtract 23 from Robot-112 you would need to break the hundred piece up into ten yellow blocks as well.

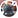








Thank you Timothy for an engaging piece about how fun maths can be. I've only read a few of your musings so far but looking forward to more things to ponder.
I have a 6 year old and 2 year old and it always played at the back of my mind to homeschool but has yet to eventuate. The eldest is attending a Steiner school at the moment which is a great fit for now. My concern is her place there is tied up to state funding and 'curriculum' requirements, so the school may go along with agendas that would be the antithesis of living a good, productive life.
I will continue reading your work and about your learning adventures in and out of the amazing sounding yurt with interest. Just wanted to share a little and show my appreciation!